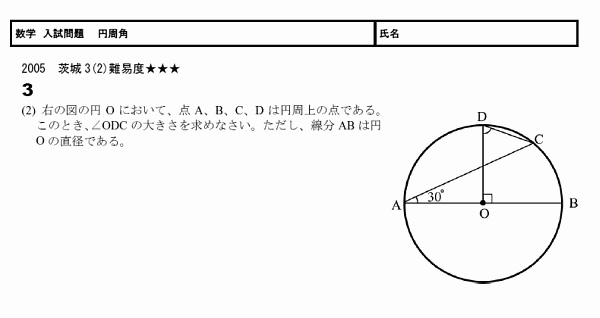
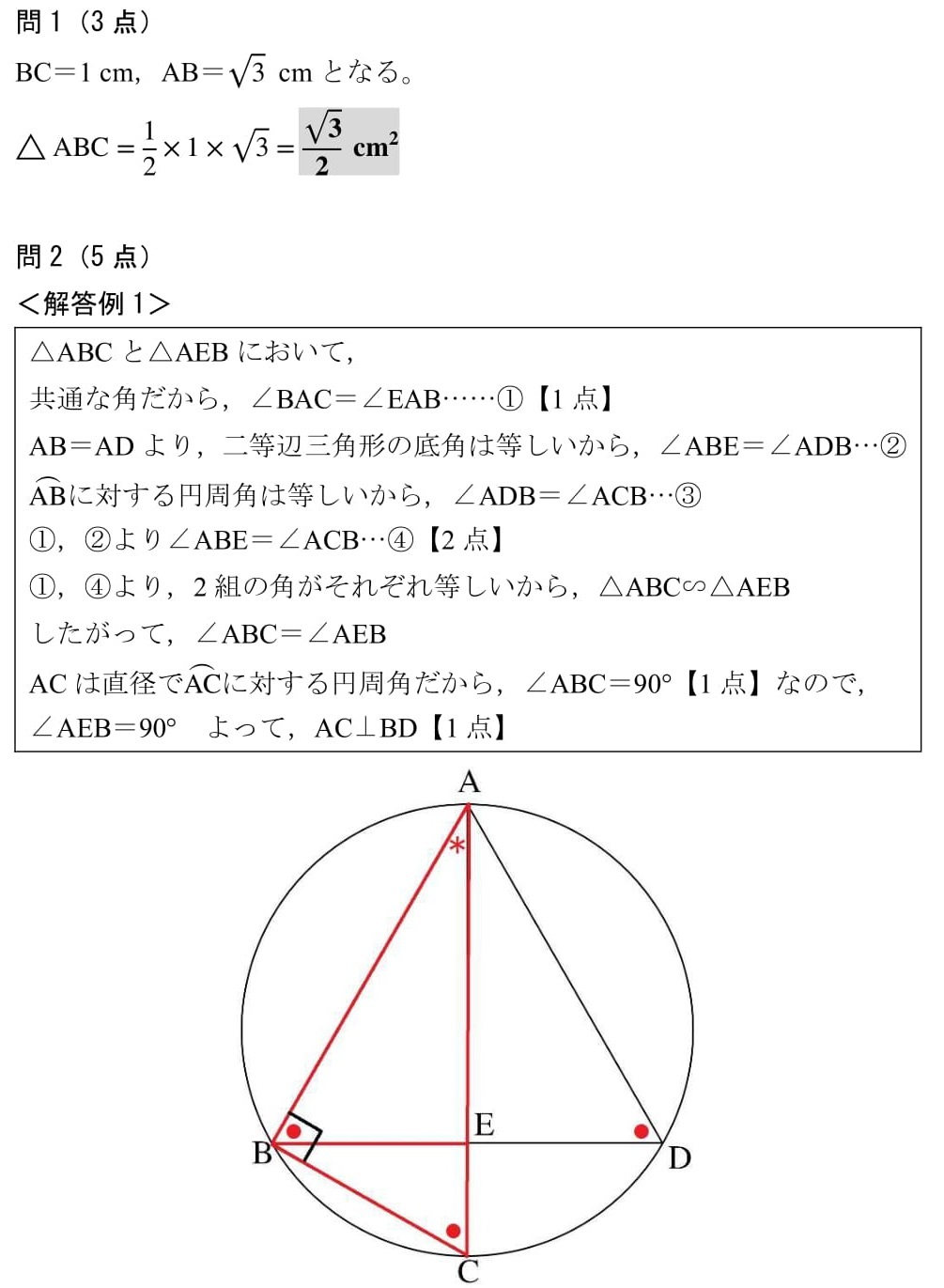
数学科学習指導案 生 徒 第3学年A組 男子19名 女子21名 計40名 指導者 教 諭 大 山 裕 之 ⅠⅠⅠⅠ 単元単単元元単元 『『『『7777章章章章 円円円円((((東京書籍東京書籍東京書籍「 「「「新しい数学3新しい数学3新しい数学3」)」」))」)』』』』円周角と中心角がどこなのかわかりません。見分け方がぜんぜんわかりません。 進研ゼミからの回答 項点が円の中心にあるのが中心角で頂点が円周上にあるのが円周角です。 円周角の定理を使って問題を解くときには与え この問題はそれを意識してみました。 特に北海道では「は? 」という証明が出されることが他県に比べて多いので,満点取りたいなら慣れておきましょう。 円周角証明の究極系 目標時間:6分 難易度:★★★★☆ 範囲:中3円周角 <問題> <PDF,解答

中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生
中3 数学 円周角 問題
中3 数学 円周角 問題-円 練習問題 円周角1 円周角2 円周角3 円周角4 円周角5 円周角6 円と接線 円と接線 2 円周角(証明) 円と相似 x=156° x=28° x=98° x=31° x=264° x=103° x=116° x=142° x=28° x=102° x=42° x=100°FdData 高校入試:中学数学3 年:円 円の角:円周角と中心角/角を分割/円周角・平行線/直径→90°/弧の長さと角/ その他 /円と合同など:正三角形・二等辺三角形/その他/円と相似:円周角/ 直径→90°/




円周角の定理 円に内接する四角形等図形の練習問題 中学 高校数学 身勝手な主張
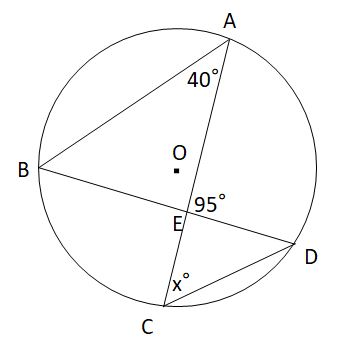
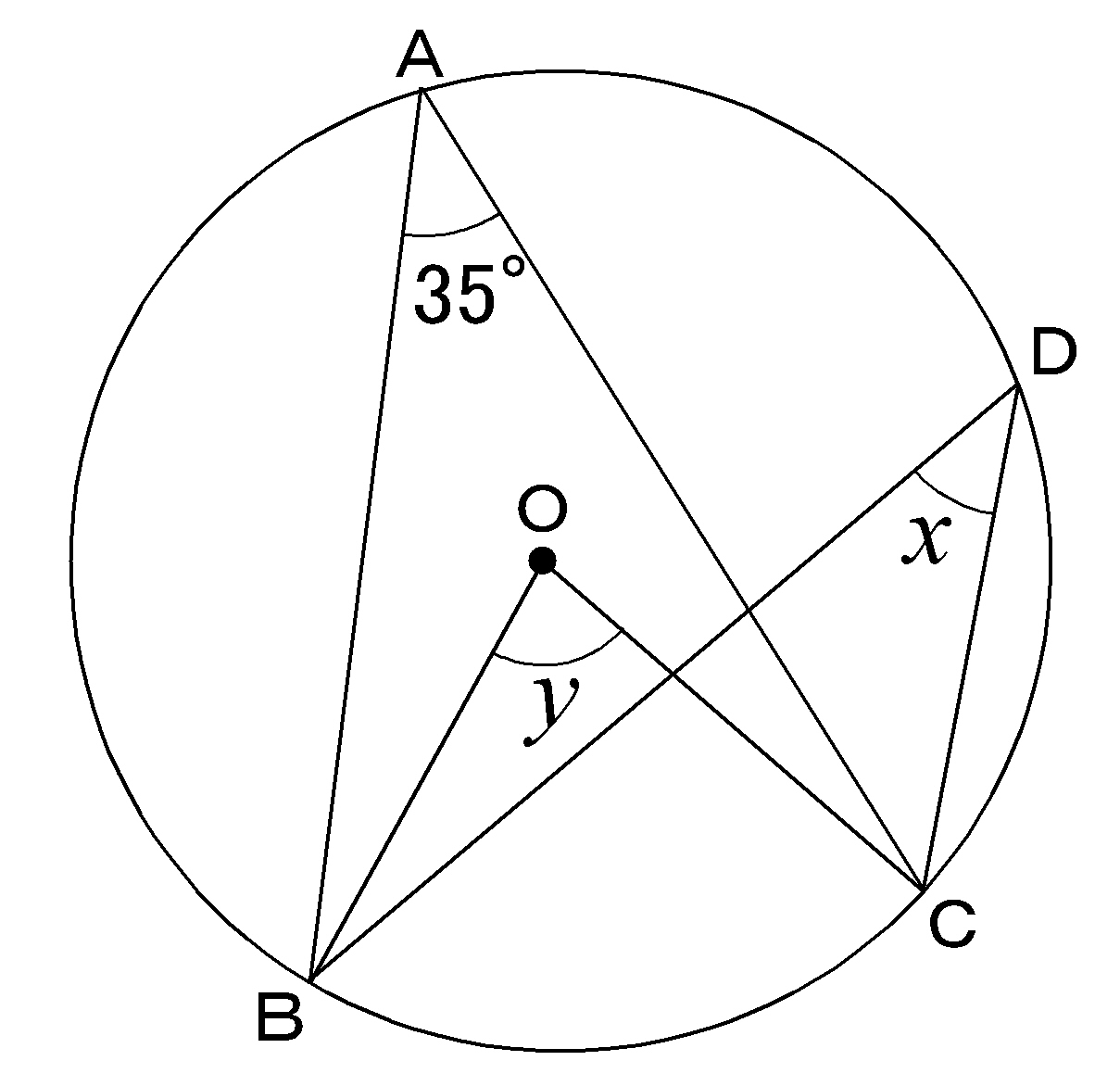
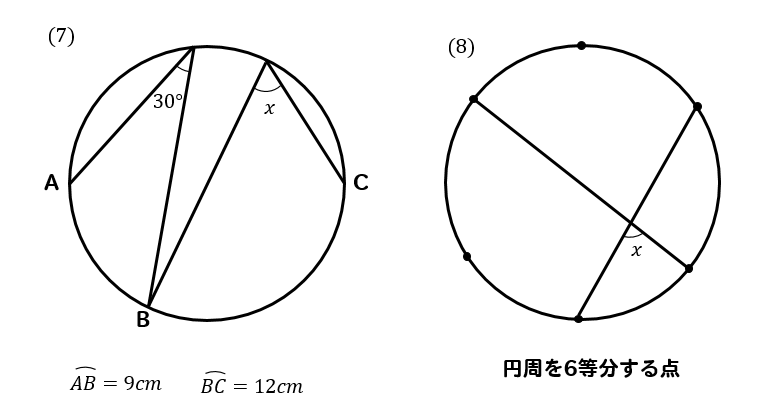
一般に,高校入試問題では「円周角の定理」を覚えているだけでは,問題は解けません.この問題では,次の2つの定理を組み合わせて解いています. (1) 一つの弧に対する円周角は等しい. (2) 三角形の内角の和は180°になる. 問題2 (1) 右の図のように,円周上に4点 A, B, C, D があり,線分 AC と線分 BD の交点を E とします。 ∠ ACD=35°, ∠ AEB=95° のとき, ∠ BAC 円周角と相似 相似が絡んだ問題なんですが、とても難しくて、 もう数学は46点満点の気持ちでいたほうがいいとかいわれました。 でも自分は数学が得意で 他の教科をカバーしたいのでなんとか数学で50点を取りたいんですが、 円周角と相似 円周角の問題に 取り組む際に、 次の3つのポイントに注意して 問題を見てみましょう。 ①弧に注目する ②直径が出てきたら 90°の円周角を探す ③補助線を引いてみる それぞれについて 説明を行っていきます。 ①弧に注目する 「円周角の問題だから
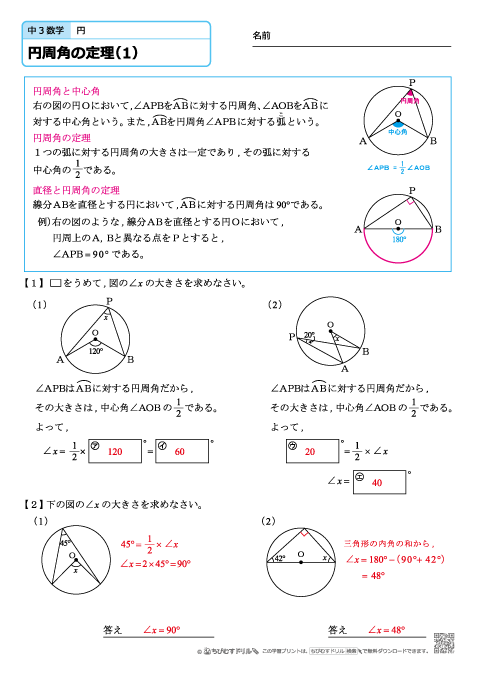
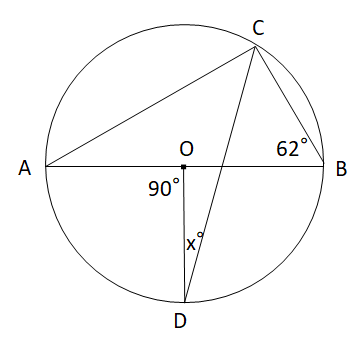
練習問題① 1 ア 円周角 イ 中心角 ウ 弧 エ 等しい ポイント 円周角の定理に関する問題だね。 円周角の定理 ① 1つの弧に対する円周角の大きさは,その その弧に対する中心角の大きさの半分である。 ② 同じ弧に対する円周角の大きさは等しい。 2数学36章 円の性質「円周角と中心角」<基本問題・解答> 解説 (1)円周角は中心角の半分なので (3)中心角は円周角の2倍なので (4)右の図のように、線分aoを引き二等辺三角形を 2つ作る。 c 二等辺三角形の底角は等しいので〇=° =45° 円周角と中心角の関係から b 解説 (1)直径に対する円周角円周角5 (発展) ACは円Oの直径、 ∠ACB=70°のとき、 ∠FECを求めよ。 A B C D E F O A B C D =53のとき, xの値を求めよ。 A B C D E F x 22° BDは円Oの直径、 ∠DBC=40°、 ∠AOD=36°のとき∠OACを求めよ。 A B C D O AC//DE, AC=DE, ∠ABC=50°のときxを求めよ。 A B C D E x
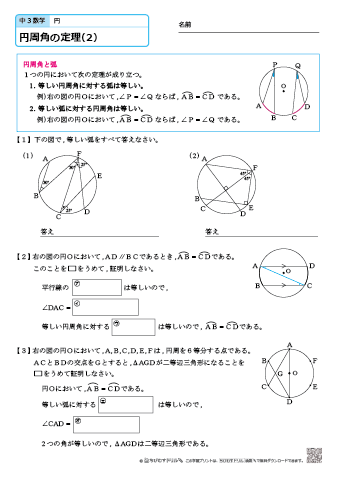
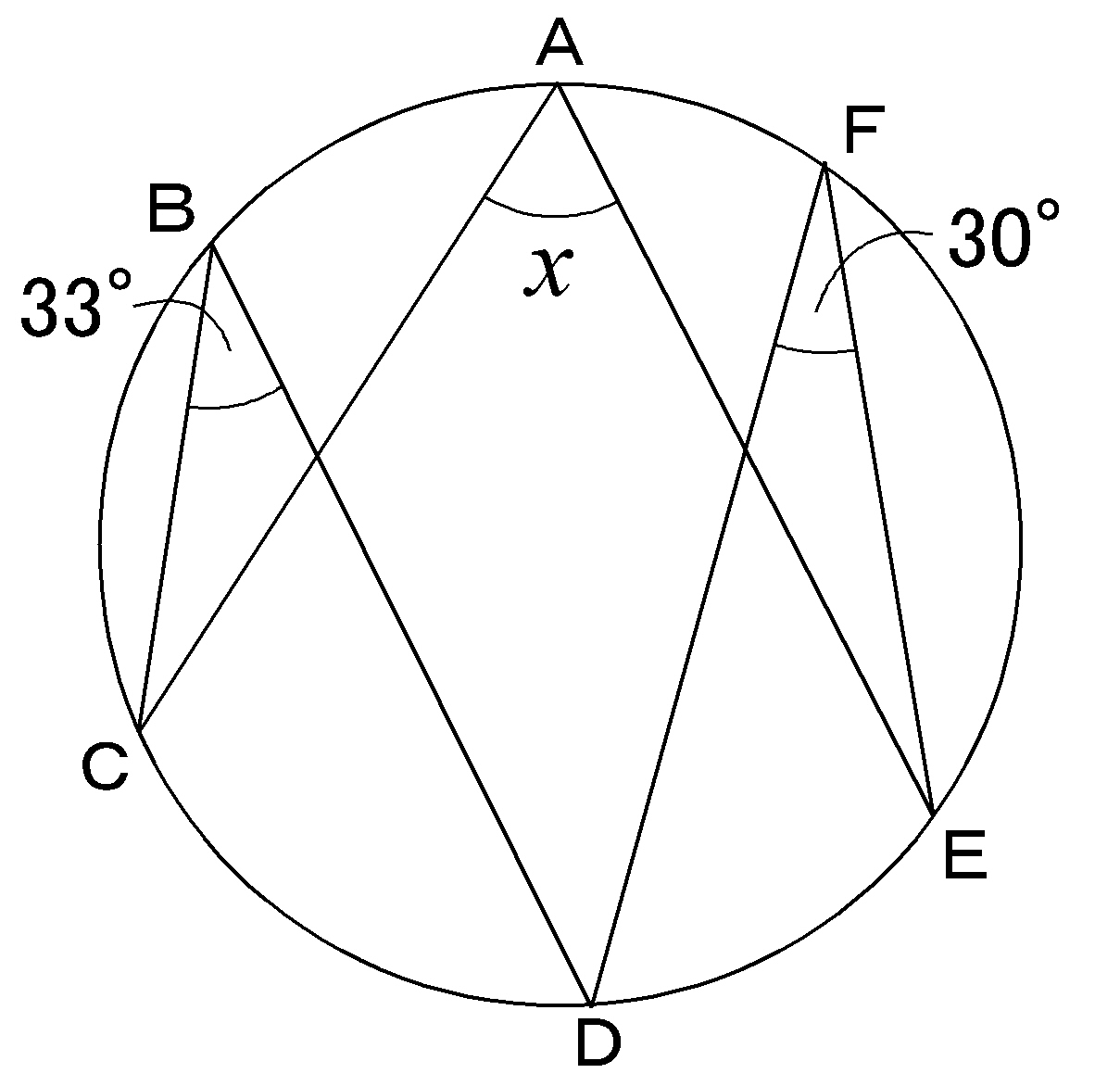
円周角と中心角の関係や、それを証明する方法を理解し、円周角の定理を活用する問題を繰り返し練習します。 円周角の定理(1) ⇒ 答え 円周角の定理(2) ⇒ 答え ⇒ 大問1の (2)の「円に内接する四角形の性質」を用いた場合の解説はこちら 円周角の定理(3) ⇒ 答え 円周角の定理(4)円周角ときたら、対になるもの、中心角です。 円周角が \(30°\) なのですから、中心角は \(60°\) です。 これって・・・正三角形の作図です! 以上、作図方法が見えましたね。 あとは手順にしたがって作図を進めていくのみです。 円周角の定理の逆を使った相似の例 さきほどの続きで直線ACと、直線BDの交点をEと置きます すると、 AEDと BECについて相似を示すことができます。 円周角の定理が使えると、対頂角と合わせることで、簡単に相似は証明できます。



円周角 無料学習プリント教材



円周角の定理 四角形
円周角の定理 (入試問題) → 携帯版は別頁 弧(こ)・弦(げん)とは 円周の一部を「弧」という. 例 右図の赤で示した部分を 弧 AB などという.(これに対して灰色で示した線分は 弦 AB という.) ※ 1つの弦により円周全体は2つの弧に分けられるよって、∠x=1°×1/2 だね。 (1)の答え 「円周角」は「中心角」の半分 になるよ。 よって、∠x=1°×1/2 だね。 (2)の答え 「円周角」は「中心角」の半分になるよ。 70°=∠x×1/2 だね。 (3)の答え この問題には中心角がないね。 円周角の定理は円の内側で考える問題でよく使われます。 同じ弧からピザが出ていた時は円周角の定理が使えます。 同じ弧を見つけることがポイントです。 補足メモ 同じ弧が別の場所にある問題を応用問題で作りたい。




円周角の定理 円に内接する四角形等図形の練習問題 中学 高校数学 身勝手な主張




円周角の定理の逆をつかった問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
円と相似 円と相似に関する問題です。 円周角の定理を利用して、相似な三角形の証明をしたり、相似比を利用して長さを求めたりします。 基本的な問題は難しくないのでしっかり確認しておいてください。 中学数学の基本から難問までの問題と分かりやすい解説を掲載した完全無料のオンライン学習ページです。 中学数学円周角の定理 例題その4 円周角超難問 中学の知識で解ける円周角を利用した超難問の問題と解説をお願いします。 それが載ってるサイトでもかまいません。 図があるとわかりやすいです。




円周角




円の性質 円周角 図形 数学 高校受験講座 東京先生
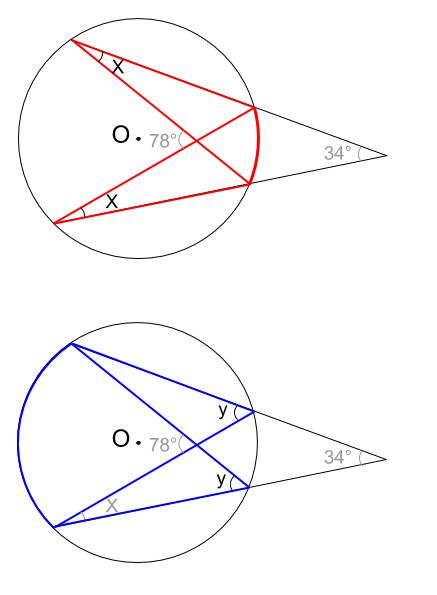
円周角 三角形の外角の関係を使う問題 円周角 補助線をひく問題 円周角と弧の比1_(円周を等分する点) 円周角と弧の比2 円 練習問題 円周角1 円周角2 円周角3 円周角4 円周角5 円周角6 円と接線 円と接線 2 円周角(証明) 円と相似点 を弦 について点 と同じ側にあるとき, 以下の内容を証明せよ。 (1) 点 が円の内部にあるとき, (2) 点 が円周上にあるとき, (3) 点 が円の外部にあるとき, 練習問題 解答へ 平面図形 円の性質 円周角 例題 練習問題円周角1 図でoは円の中心である。∠aob=78°のとき∠acbを求めよ。 更新履歴 リンク お問い合わせ 歴史用語集 地理用語集 歴史問題 地理問題 公民問題 英語問題 数学問題




世界一わかりやすい数学問題集中3 6章 円の性質




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
FdData中間期末過去問題中学数学3年(円周角と中心角/円周角の定理/接線) Author Fd教材開発 Created Date 4/9/19 PM 中3数学 円周角(ブーメラン型四角形)まとめと問題 円周角の問題を解くとき、円周角の定理がわかっていても、どう解いたらいいのか悩むことも多いです。 今回はそんな円周角の中でも、ブーメラン型の四角形(凹四角形)の円周角について学習します。 弧の比から円周角を求める問題についても扱っています。 ブーメラン型四角形の円周角問題の解き方を知り数学の学習の中でも証明が日常の役に立つことを実感し ている生徒は少ない。また中学校の数学の中で,円周角の定理を日常生活の中で用いる 場面を取り上げることはほぼないと感じる。そこで円周角の定理を用いた証明問題を取 り上げる。




数学 中3 円周角 中学生 数学のノート Clear




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ
円周角の定理の解説・問題の解き方 三角形・四角形などの角の大きさについてはこれまで扱ってきましたが、ここから円と多角形が組み合わさった、さらに複雑な問題を扱うようになります。 覚えるべき定理はいくつかありますが、最も重要なのが今回解説する『円周角の定理』です。 今回は円周角の定理だけではなく、これに関連した定理を紹介して、問題を中学数学 円周角・中心角 トップページ > 中学3年生 > 円周角・中心角 2年生問題集 ( excel 利用) が完成しましたので、よろしければご利用くださいね (全1539問) ( 有料 )。 1年生問題集は引き続き ( 無料 )です → ダウンロードページへ 中学1年生 課程へ対する円周角は90° となる。 o 円の直径の円周角 半円の弧 円周角 180° 問題文に「垂直・90°」とあったら 半円の弧に対する円周角は90° となることを利用 条件反射 円と接線の角 接点を通る半径は 接線と垂直に交わる。 o 接点 接線 「線分の中点を求める
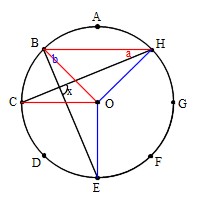



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ




中3数学 円周角 ブーメラン型四角形 まとめと問題
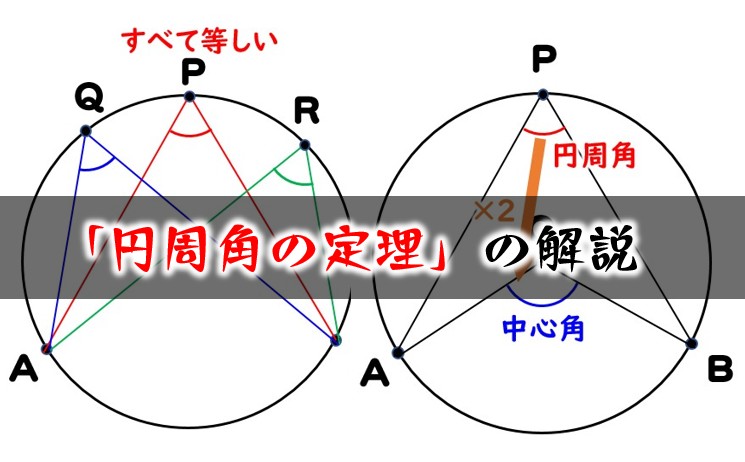
円周角の定理とは まず、問題を解いていく上で知っておいて欲しい知識がこちら 同じ弧に対する円周角の大きさは等しい 同じ弧に対する中心角の大きさは円周角の大きさの2倍 直径に対する円周角は90° 弧の長さが等しければ、円周角・中心角の大きさは等しい 同じ弧でなくても長さが等しければ、円周角、中心角は等しくなります。 円周角、中心角の大きさは まとめ:円周角の定理はしっかり覚えよう! どうだったかな? 円周角の定理がどんなものか 理解できたかな? どこが円周角で、どこが中心角なのか ぱっぱと頭の中で分かるようになるのがカギだね。 円周角の定理を使った問題をくりかえしやってみてね。円周角の問題が解けるようになるためには? ここまで円周角を詳しく見てきましたが、どのようにしたら「円周角が得意!」と言えるようになるのでしょうか? それを言えるようになるためには「 円周角の定理をパッと言えるようになること 」が必要です




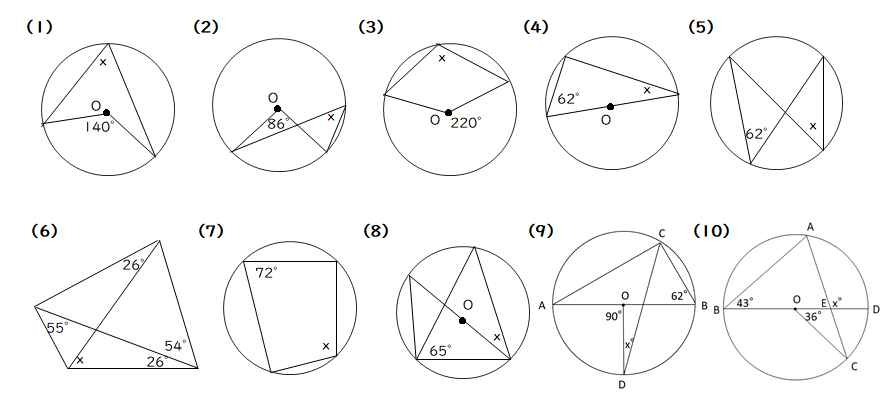
円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者



中3数学 円周角の定理を使った定期テスト予想問題 Pikuu
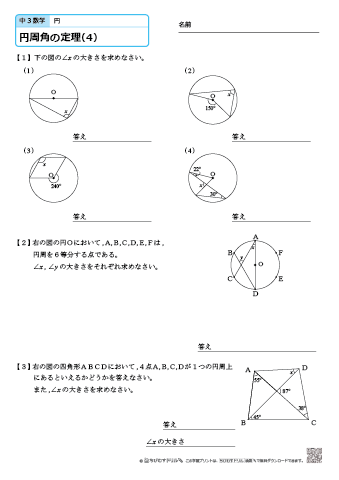



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生



中3数学 円の性質2 円周角と中心角 すべて無料 星組の中学数学講座



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生



円周角の定理 練習問題 角度がわからない 苦手な数学を簡単に



中3数学 円周角の角度を求めるポイントと練習問題 中学生勉強サイトあかね先生



数学a 円周角と中心角の関係の使い方とコツ 教科書より詳しい高校数学




中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生



意外と解けない円周角の定理 中3レベルの数学問題 暇つぶしに動画で脳トレ




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者



1




円周角の定理 円周角と中心角の関係は中学や高校でよく出るぞ 中学や高校の数学の計算問題



数学問題 大人は意外と悩んでしまう円周角の定理 ネタファクト



中3数学 円周角の角度を求めるポイントと練習問題 中学生勉強サイトあかね先生




6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく



円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典




円周角 無料学習プリント教材



数学 円周角の定理 静岡県公立高校入試問題



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく



中学3年数学練習問題 円周角の定理の基本



中学3年の数学の円周角の定理問題なのですが よくわからな Yahoo 知恵袋
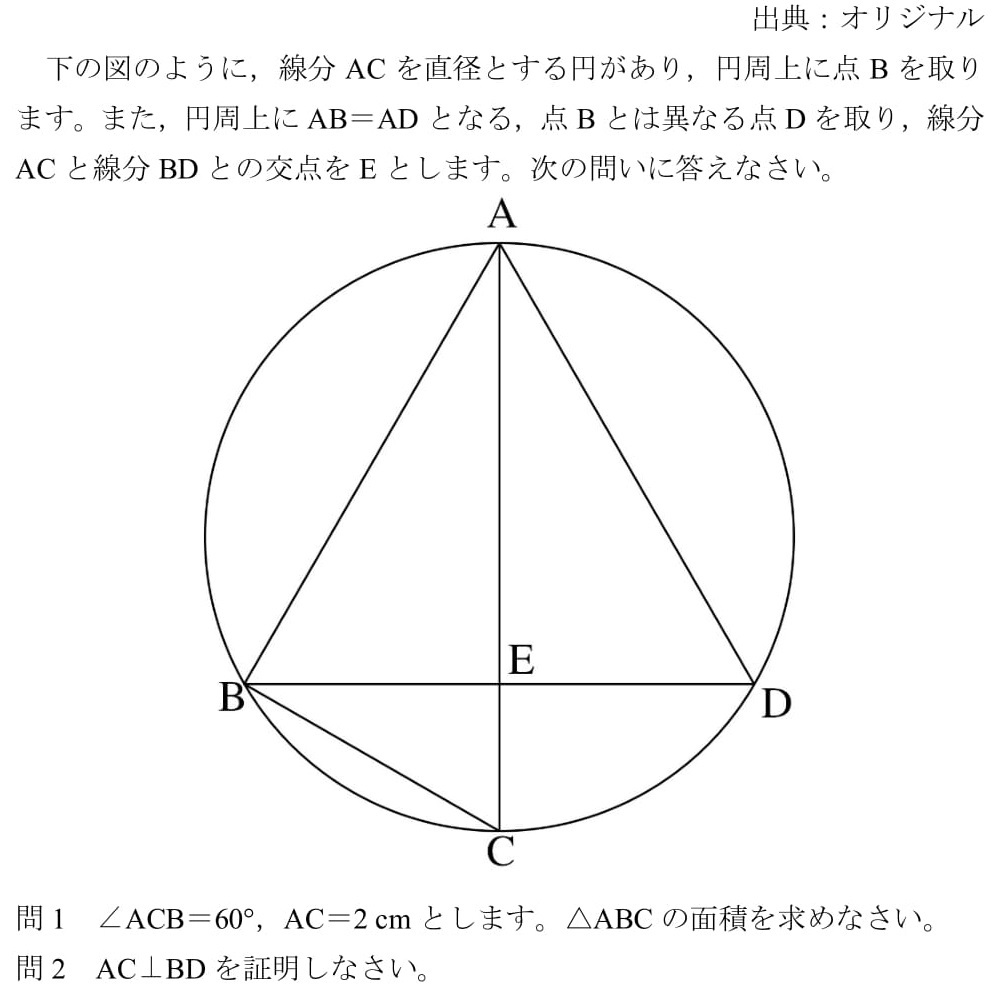



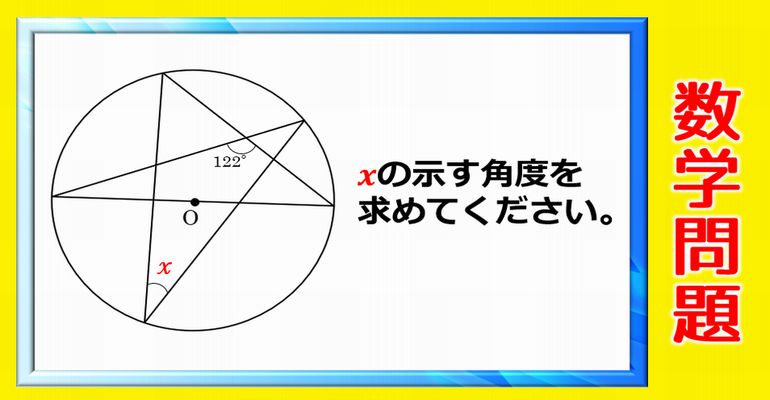
円周角証明の究極系 オリジナル 高校入試 数学 良問 難問
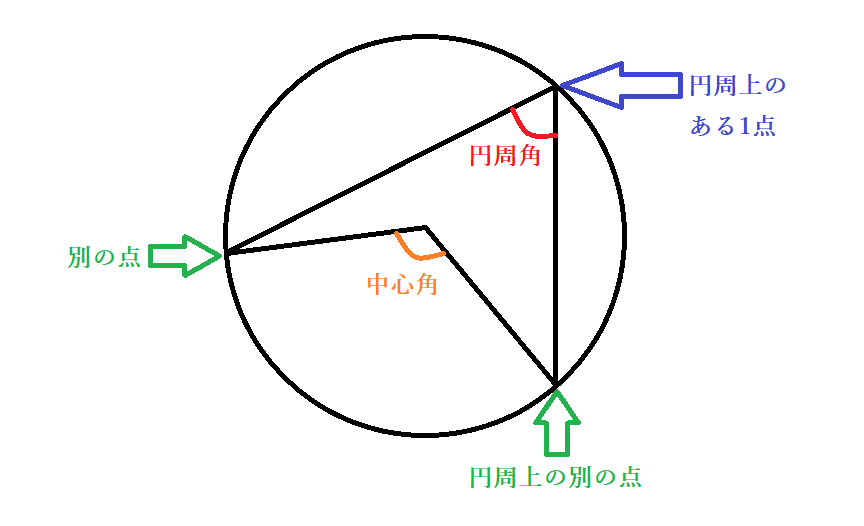



中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの幸せblog
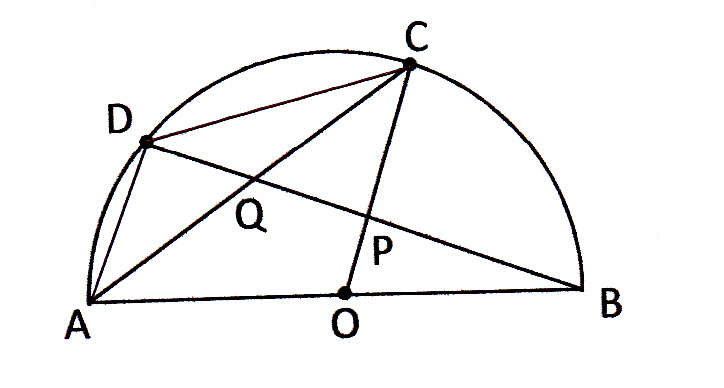



円周角の定理を使った相似の証明の解き方 現役塾講師のわかりやすい中学数学の解き方



1
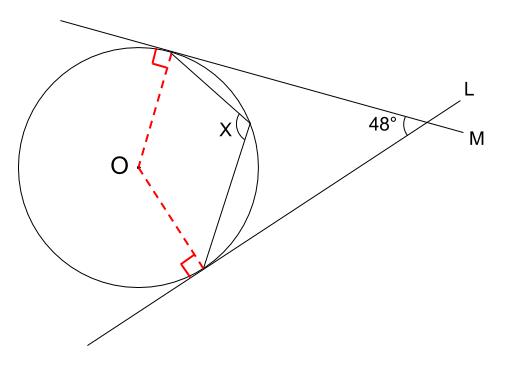



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su




円周角の定理の逆 無料で使える中学学習プリント
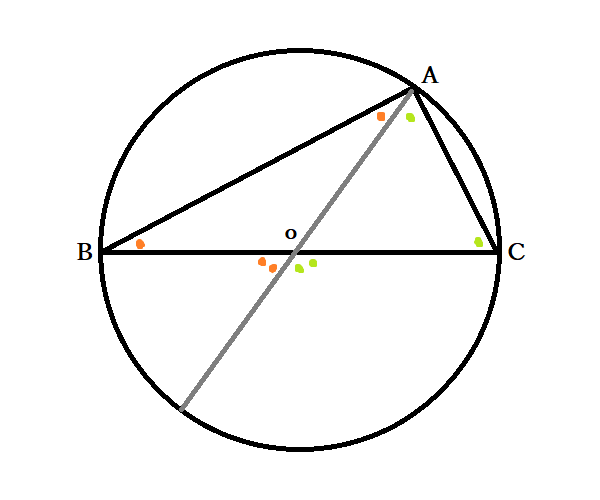



中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの幸せblog
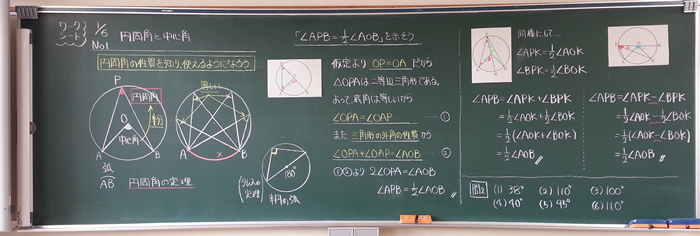



授業実践記録 数学 第3学年 数学的な見方 考え方を養う 円周角の定理 の授業 動的幾何学ソフトウェア Geogebra を用いて知識を拡張 統合する 啓林館
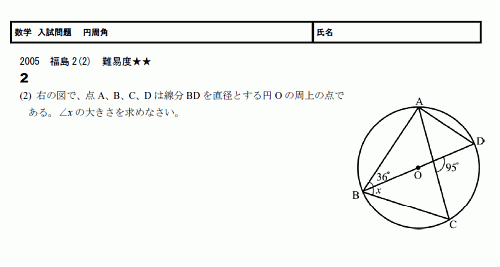



円周角 無料学習プリント教材




中学3年の数学 動画 円周角の定理 基本編の問題 19ch




これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




円周角の定理の基本 計算 無料で使える中学学習プリント




中3数学 円周角 ブーメラン型四角形 まとめと問題




数学 円周角の問題を解くコツ




円周角 補助線を引く問題
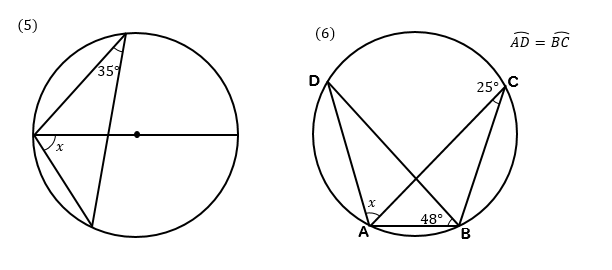



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ



数学 円周角の定理 岩手県公立高校入試問題



Wordで使える 円周角の問題の図 その1 Wordで数学問題プリントを作ろう



Wordで使える 円周角の問題の図 その2 Wordで数学問題プリントを作ろう




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



円周角証明の究極系 オリジナル 高校入試 数学 良問 難問



Math 円 4 円周角の難しい問題を解くコツ 働きアリ The 2nd



中学3年 数学 円周角の定理 問題 Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト



円の性質 円周角 図形 数学 高校受験講座 東京先生




中学3年数学練習問題 円周角の定理の基本



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ




中学3年の数学 動画 円周角の定理 少し応用編の問題 19ch



1




数学 中3 57 円周角の定理 少し応用編 Youtube




数学 中3 59 円周角の証明チャレンジ Lv 1 Youtube




円周角の定理と証明 中心角の求め方を詳しく解説 Rikeinvest



円周角の定理の解説 問題の解き方 数学fun



円周角の定理 練習問題 苦手な数学を簡単に




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



円周角の問題 中学から数学だいすき




高校数学a 共円条件 4点が同一円周上にある条件 受験の月




Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ




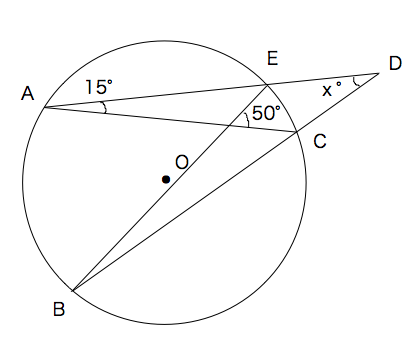
Xの角度の求め方を教えてください 3 と 5 です 円周角の問題です Clear



1
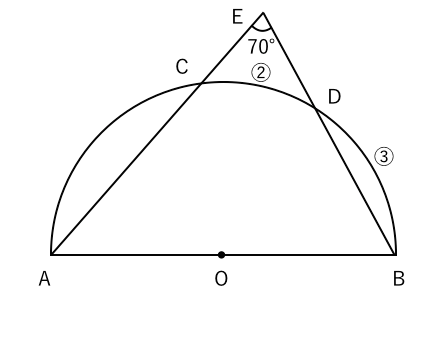



円周角と比の問題 苦手な数学を簡単に




円周角の定理 円に内接する四角形等図形の練習問題 中学 高校数学 身勝手な主張




中3数学 円周角の定理を使った定期テスト予想問題 Pikuu




世界一わかりやすい数学問題集中3 6章 円の性質
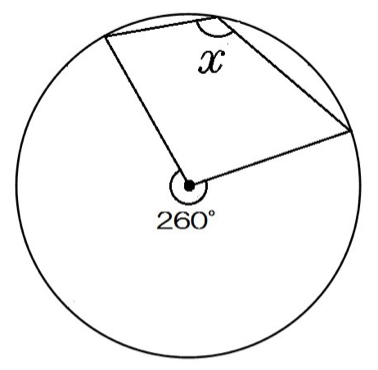



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




円周角の定理とは 必ず押さえたい7つのポイント 遊ぶ数学



円周角




中3数学 円周角の定理 良難問とその解説 定期テストや高校入試に レオンの中学数学探検所




中3数学 円周角の定理の逆 の重要ポイント 映像授業のtry It トライイット
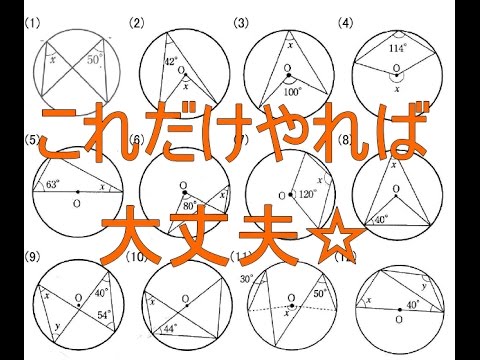



円周角の定理と中心角 中学3年数学 Youtube



円周角と中心角 中学から数学だいすき
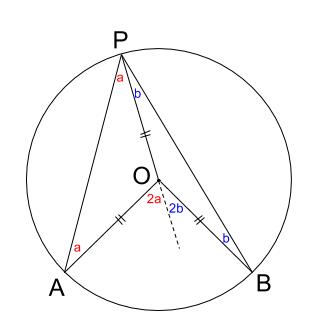



中学数学 円周角の定理はなぜ成り立つのか 中学数学の無料オンライン学習サイトchu Su
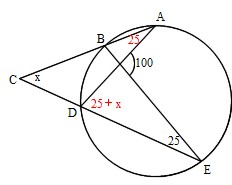



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ




円と角度のチェックテスト2 円周角を求める発展問題 難しい問題もあります Youtube
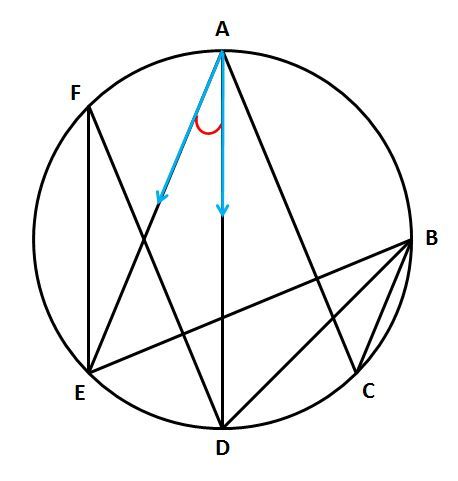



円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室
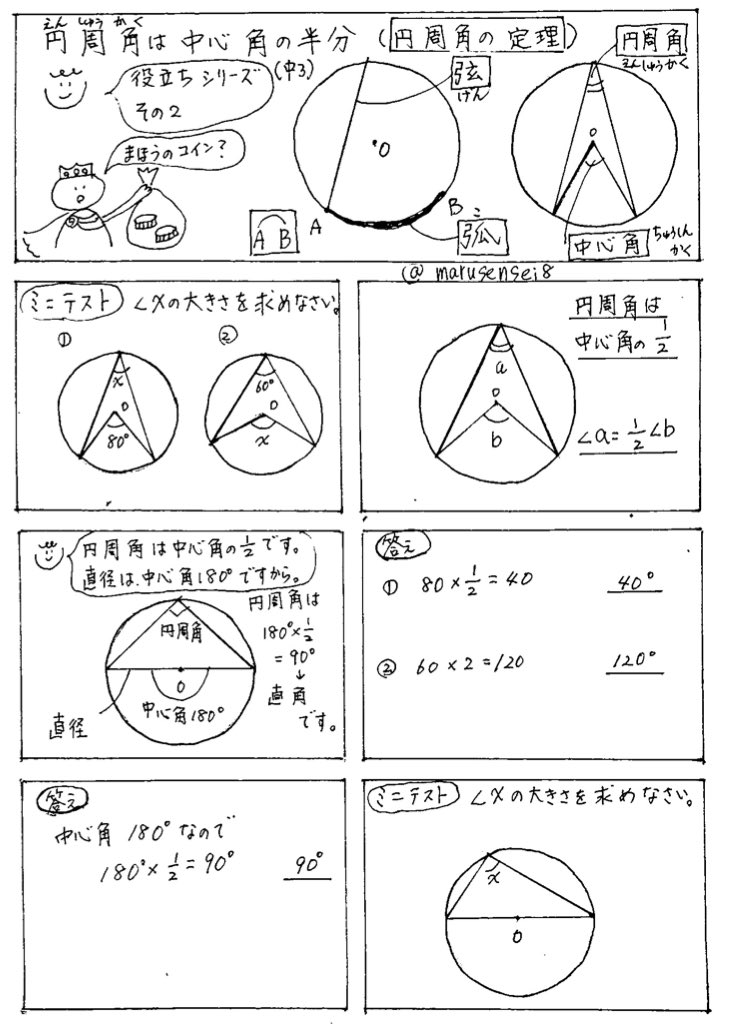



円周角の定理
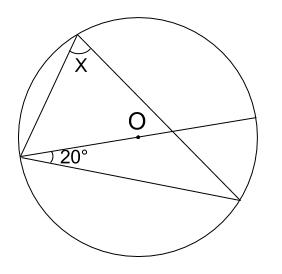



中学数学 円周角の定理 例題その3 中学数学の無料オンライン学習サイトchu Su




円周角の定理はこれで完璧 定理の証明と様々な問題の解法
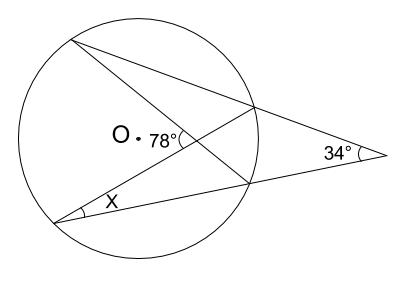



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su



高校入試 英語 数学 円 重要問題




円周角の定理の基本 計算 無料で使える中学学習プリント




中3 数学応用 円周角の定理 証明 中学生 数学のノート Clear




数学 中3 56 円周角の定理 基本編 Youtube




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




中学3年数学練習問題 円 円周角の定理 内接円 接弦定理 の問題




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学



0 件のコメント:
コメントを投稿