√100以上 3次式 因数分解 公式 183787-3次式 因数分解 公式

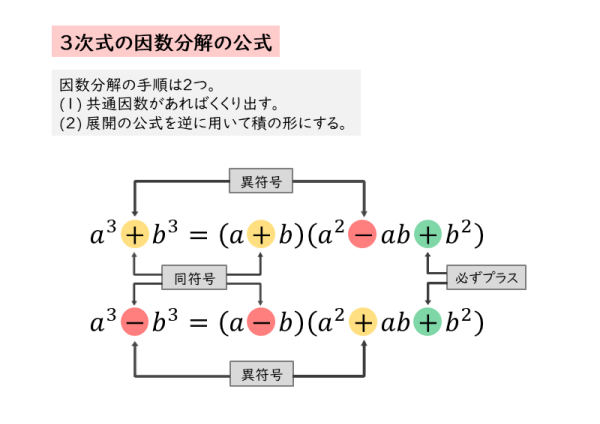
3次式の因数分解3次式を因数分解するとき、公式の適用をまず考えます。公式が適用できないとき、因数定理を用います。例題1有理数の範囲で、\(x^37x6\) を因数分解しなさい。解説公式で因数分解できないので、因数定理を使います。\(P(x)=x^37x6\) とおきます。 \(x^37x6=(xk)Q(x)\) と因数分解されるので、このような \(k\) を因数定理で探します。\(P(k)=0\) を満 3次式の因数分解の公式利用 3乗の因数分解（展開）公式 3596k 件のビュー; ３次式の因数分解の公式 a3 b3 = (a b)(a2 − ab b2) ⋯① a3 − b3 = (a– b)(a2 ab b2) ⋯②

一般三次方程式的解 配立方 Youtube

3次式 因数分解 公式

3次式 因数分解 公式- 因数分解 式の計算 更新日時 四次式の因数分解（または方程式を解く）に関する問題は，以下の5パターンがあります。 パターン1A：普通に因数定理が使える場合 パターン1B：二次式×二次式に分解できる場合 パターン2：相反方程式 パターン3高校数学Ⅰで習う2次式と3次式の展開公式を簡単に振り返り問題演習を行う．採点と解答付き === 読者が配色を変更したい場合 === 外側の色を変えるには，次の色をクリック 内側の色を変えるには，次の色をクリック 標準文字色を変えるには，次の色をクリック 鼠 銀 黒 青 紺 茶 緑 桃

Sqrt2right Pa43 Left 1r Descubre Como Resolverlo En Qanda

 ここは、 x についての3次式ですが、 y, z については2 ここでは、三次式の因数分解の公式の応用として、対称性のある式の因数分解を見ました。1つの文字について整理しながら、今まで使った公式を何度も用いているだけですが、ゴールまでたどり着くのはハードルが高いですね。※数学において誘導や利用して、というのは必ずそれを使うように問題がつくられている。（使わない場合はそれは別解、ということ。使えば(おそらく)楽になるので使うべき。) (1) \(a^3b^3=(ab)^33ab(ab)を利用して, \\~~~~~a^3b^3c^33abc~~を因数分解せよ\) x 3 6 x 2 3 x 12 x^36x^23x12 x 3 6 x 2 3 x 12 が因数分解できないことを示せ 解答 ( x − a ) (xa) ( x − a ) を因数に持つならば a a a は 12 12 12 の約数である （→方程式の有理数解） ので全部調べればよいのだが，めんどうなのでアイゼンシュタインの定理を使う。

 たすき掛けの因数分解！コツを学んでやり方をマスターしよう！ 4乗！？複二次式の因数分解の解き方！途中式をていねいに解説するぞ！ 3次式の因数分解！公式とやり方について問題を使って解説！ ←今回の記事;途中式の2、3行目を見てもらうとわかりますが、 \(a\) の1次式が因数分解できるというなら \(a\) の係数に必ず共通因数が入っているはず です。1次式の因数分解は「共通因数でくくる」という手段しか存在しないからです。（2次、3次などなら公式利用動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru

 2 2次式の因数分解 まず、因数分解するに当たって、次の数は覚えておきましょう。 1 , 4 , 9 , 16 , 25 , 36 , 49 , 64 , 81 , 100 , 121 , 144 , 169 , この数にはどのような特徴があるかわかりますか？ そうですね、 自然数を2乗した数 になっています。 例えば、\(1=1^2\) , \(4=2^2\) , \(9=3^2\) ですね。 これらの3文字3次式の因数分解 立方の公式1でも触れたが、 (a b)3 を展開すると (a b)3 = a3 3a2b 3ab2 b3 であるから a3 b3 = (a b)3 − 3a2b − 3ab2 ⇔ a3 b3 = (a b)3 − 3ab(a b) が成り立つ。 これを用いることにより、 a3 b3 c3 − 3abc は、次の例題でみるように因数 6次の 因数分解 この 因数分解 を2通りで行ってみます。 という 因数分解 の公式が得られます。 まぁ、こんなマワリクドイことをしなくても、以下のように 因数分解 できますけどね： « commonsmath 解読 (11) 複素数 Complex 倭マン's Math (7) FractionField, Frac

一元三次多项式因式分解的两种方法 Longlongqin的博客 程序员宅基地 一元三次因式分解步骤图 程序员宅基地

高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium

係数が実数の2次式の因数分解について，2次式の因数分解の公式と前節の定理34 とを組み合わせると次の定理が導かれます（証明は省きます）． 定理35 定数a, b,c が実数を表し，a 6=0 のとき， x の2次式ax2bxc が係数が実数の範囲で1次式の積の形に因数分解できる ⇐⇒ b2−4ac ≥ 0質問数学（高校）：特殊な3次式の因数分解 質問数学（高校）：特殊な3次式の因数分解 数学Ⅰ, 数学Ⅱ 〔質問〕 a 3 (b－c)＋b 3 (c－a)＋c 3 (a－b) の因数分解がわかりません 〔回答〕 まずは、どれかの文字だけに注目して整理しましょう！ 解法 このような複数文字が登場する式の因数== 3次以上の因数分解 == （例題→選択問題） ※ 3次以上の式の因数分解を行う強力な方法として「因数定理」があるが，これは数学iiで習う．数学iではもっと簡単に「因数分解公式」「置き換え」などで因数分解できるものだけを扱う．

因数分解公式の導出 3次式 受験数学って暗記 仮 高校受験 大学受験 楽天ブログ

1

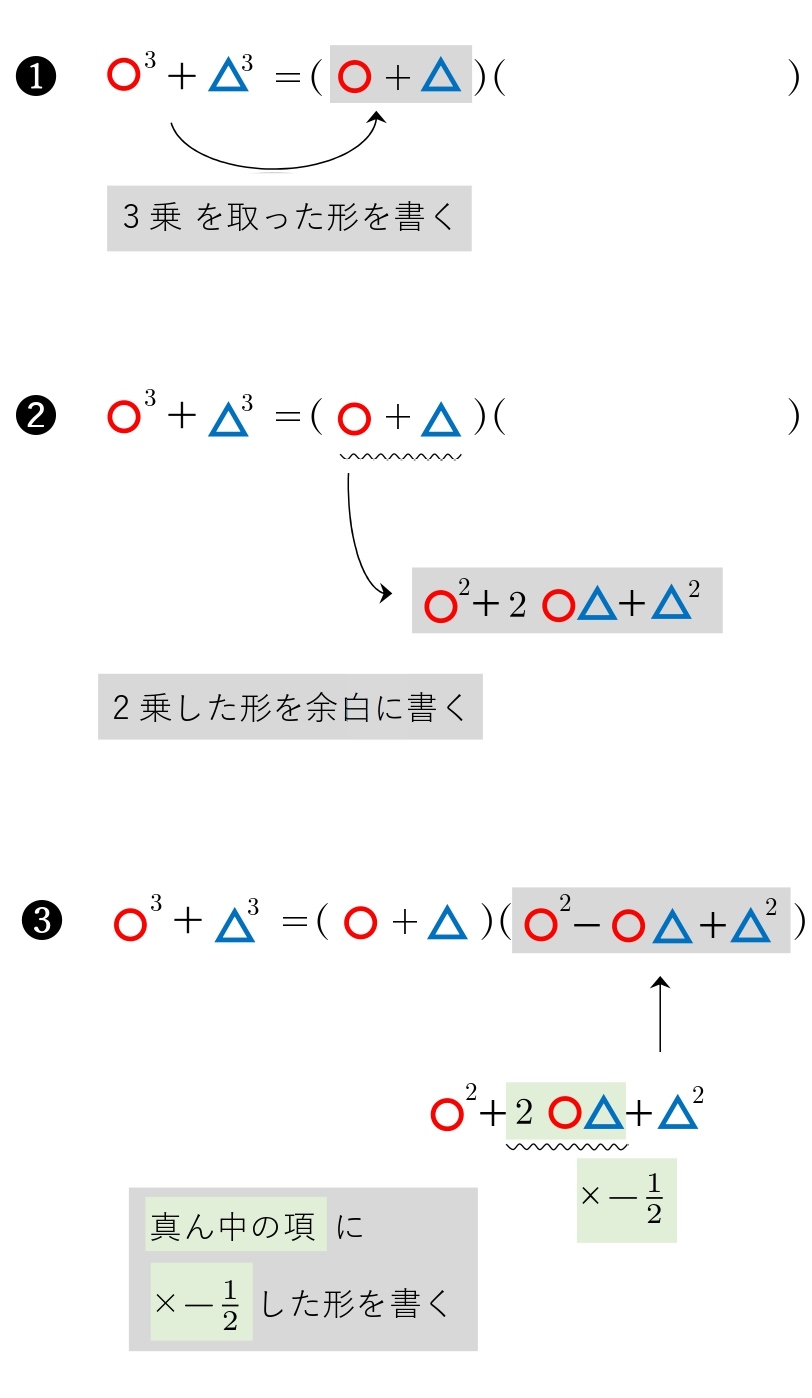
 3次式の因数分解でよく使う4つの公式 2次式の公式も、3次式の公式も、「覚えているだけ」では、まったく役に立ちません。 例えば「$x³3x²3x1$ を因数分解しなさい。」という問題。 10秒以内に答えられますか？ この問題、「$y=1$ になっている！」という点に気が付ければ、①の公式を使って簡単に解くことができるんです。単元「式と証明・高次方程式」において3次式の因数 分解の公式を基に，x3 工夫された3次式の因数分解などが，数学Ⅱの教科書 では扱われている。 xn－1の因数分解の背景には，大学で学ぶ代数学 の多様な理論が存在する。（岩永，02，Tignol， 06） 例えば，「複素数体上の既約多項式は 3文字3次式の因数分解 こんな感じの式。 この式を因数分解してみる。 こんな感じになる。 公式として覚えるときは、また少し式を変形させる。 覚えるときはこの形で覚える。 定義を知る この公式は覚えておくべきだし、導けるようにしておくべき。 まとめ

3次の因数分解の公式 数学が嫌いなんです

因式分解

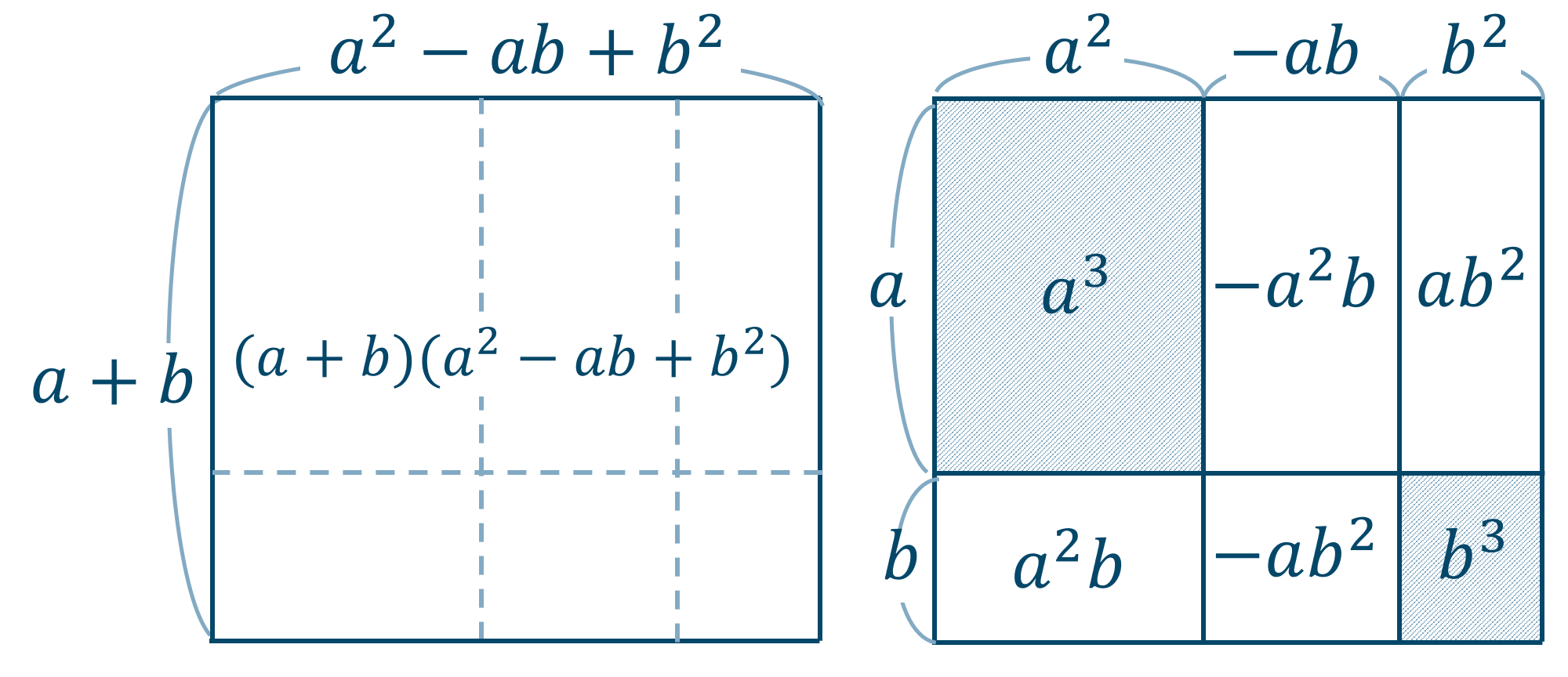
 こうして、3乗の展開・因数分解の公式は、立方体の分割で考えることができることがわかりました。 3乗引く3乗の公式 続いて、3乗引く3乗の公式について考えてみましょう。\ x^3y^3 = (xy)(x^2xyy^2) \左辺を見ると、一辺が x の立方体、一辺が y の立方体の体積を考えればよさそうです。上と似 高校数学Ⅰ3次式の展開・因数分解（公式・覚え方・計算方法） 21年4月28日 このページでは、 数学Ⅰの「展開・因数分解の公式」についてまとめています。3次式の因数分解公式があるならば、逆は展開の公式になります。 展開の公式を覚えておけば、因数分解もできるようになるのでぜひ押さえておきましょう。 シータ 展開ができれば因数分解もできる 今回は3次式の展開の公式について紹介します。 では順を追ってまとめていきます。 記事の

一元二次方程的解法 公式法 因式分解法和十字相乘法基础练习 一元二次方程交叉相乘 艾帝网

因式分解

4次式の因数分解の公式 x 4 x 2 1 = (x 2 x 1) (x 2 − x 1) ⇒ 導出計算 ホーム>>カテゴリー別分類>>数と式>>整式：因数分解の基本公式 最終更新日： 16年12月12日 ページトップ 高校の数学Ⅱで扱う文字式の展開の基本問題から応用問題までの練習です。 主に変形に利用するのは3次式の展開公式です。 展開は乗法公式を使わなくても必ずできますが、手順によっては処理が早くなる問題も少なくありません。 ある程$1729 = 1^312^3 = 9^310^3$ は $2$ 通りの立方数の和として表される最小の正の整数である 「インドの魔術師」という異名を持つ数学者 s・ラマヌジャンは療養中, g・h・ハーディーが見舞いに訪れた際に, 「乗ってきたタクシーのナンバーは $1729$ だった さして特徴のない数字だったよ」 という

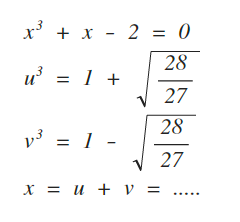
高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium

1

高校講座HOME >> 数学Ⅱ >> 第2回 第1章 方程式・式と証明 整式・分数式の計算 3次の乗法公式と因数分解 (1) 数学Ⅱ ラジオ第2放送 毎週 水曜日因数分解電卓 複雑な式を単純な因子の積に変換します。この因数分解電卓は、任意の変数を含む多項式だけでなく、より複雑な関数を因数分解することができます。 数式の書式を表示 式の因数分解例 数学ツール 微分電卓 積分電卓 積分計算 極限の計算 級数計算機 方程式を解く 式の簡略化→3乗の因数分解公式5つと例題 ～めったに使わない、四乗の公式～ $x^44x^3y6x^2y^24xy^3y^4$$=(xy)^4$ $x^44x^3y6x^2y^24xy^3y^4$$=(xy)^4$ $x^4y^4$→これ以上因数分解できない $x^4y^4=(xy)(x^3x^2yxy^2y^3)$ ～高校数学で習う難しめの公式～ $a^2b^2c^22ab2bc2ca$$=(abc)^2$ $a^3b^3c^33abc$

数学ii 公式まとめ 高校生 数学のノート Clear

これらの公式がなかなか覚えられないです どのように覚えるのがよいのでしょうか Clear

 あなたは部分分数分解を単なる「式の変形」だと思い込んでいませんか？ 実は数学b の数列の単元や数学3の積分計算でとてもお世話になる、大切な式変形なんです。 今回は、その「部分分数分解」を、公式・やり方だけでなく数列の問題への応用を詳しく解説しました!3次方程式まとめ（解き方・因数分解・解と係数の関係） 2908k件のビュー 数学Ⅰ三角比sin cos tanの公式まとめ（表・変換Course Summary 高校数学（数I) 因数分解、基本編、たすき掛け編、応用編、3次式の公式編 みなさん、初めまして。 本講座を担当している葉一（はいち）と申します。 私は元塾講師なのですが、塾講師として勤務していた期間に何度も この言葉を耳にし

如何因式分解三次多项式 12 步骤

解一元二次方程的基本方法 公式法 因式分解法 直接開平方法 每日頭條

4次式の因数分解の公式 x 4 x 2 1 = (x 2 x 1) (x 2 − x 1) ⇒ 導出計算 ホーム>>カテゴリー別分類>>数と式>>整式：因数分解の基本公式 最終更新日： 16年12月12日 ページトップ 利用規約 google translate (English version)

三次函數因式分解計算器factoring Cubic Function Calculator 學校沒有教的數學 學校沒有教的數學

3次式の因数分解 公式とやり方について問題を使って解説 Youtube

高校数学 数 11 因数分解 ３次式の公式編 Youtube

2 8x3 36x2y54xy2 27y3 Descubre Como Resolverlo En Qanda

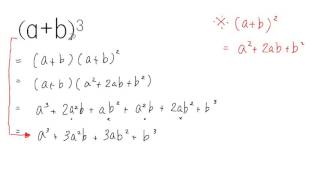
2 三次方程式展開

一元三次方程快速解法 高三网

5項式的因式分解第二種解法 X 2x X 3x 2x 1 先思考 每日頭條

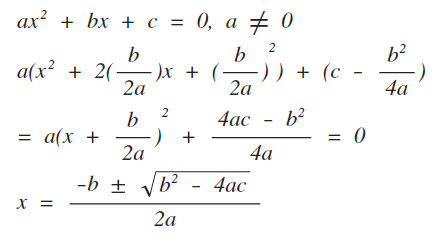
高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium

因数分解3 次 因数分解3次

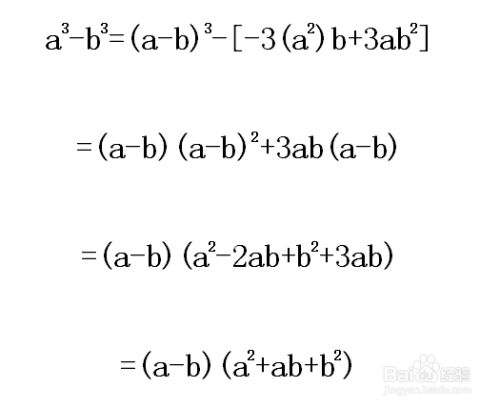
X的三次方减一怎么因式分解 百度经验

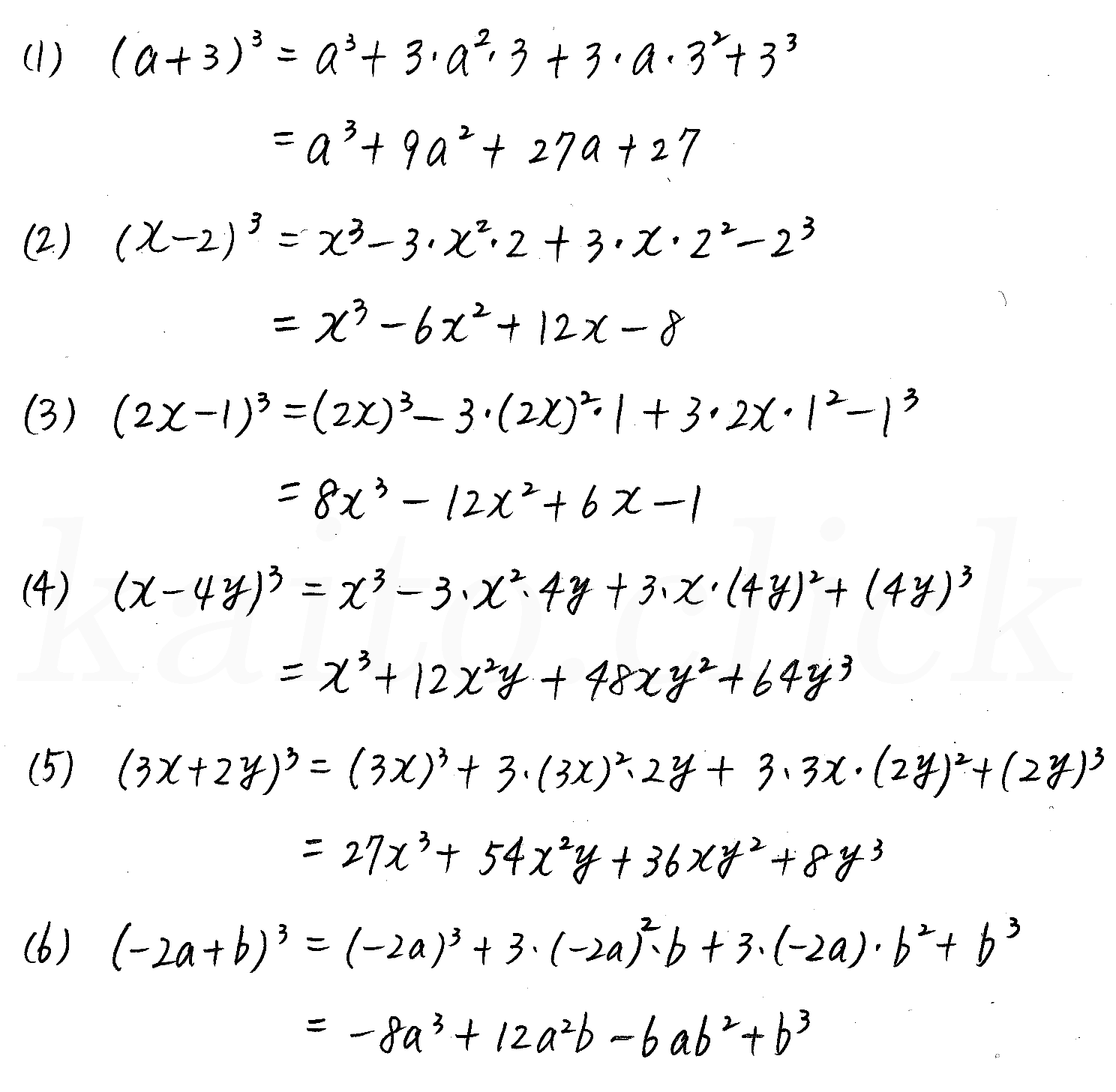
50 因数分解3 次

三次方程 三次方程的英文名是cubic Equation 指的是一種數學 百科知識中文網

数学 ３次式の因数分解の公式の使い方とコツ ページ 2 教科書より詳しい高校数学

1 4乘法公式与因式分解

３次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ

３次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ

X3次方 Y3次方 怎么因式分解还有因式分解的思路 作业 慧海网

因式分解公式计算机

初二数学因式分解 二 运用公式法 例题解析及课后训练 初中数学 学习资料大全 免费学习资源下载

乘法公式和因式分解练习题 Doc 牛牛文库niuwk Com

3 Bar3 A3b3left Abright Descubre Como Resolverlo En Qanda

Search Q E4 B8 E6 Ac A1 E6 96 B9 E5 85 Ac E5 8f Tbm Isch

Sqrt2right Pa43 Left 1r Descubre Como Resolverlo En Qanda

高校数学 ３次式の展開 因数分解 公式 覚え方 計算方法 学校よりわかりやすいサイト

03公式法之平方差公式因式分解初中数学初二 Youtube

3乗の因数分解 展開 公式 理系ラボ

完了しました 因数分解3 次 ニスヌーピー壁紙

高校数学 数 勉強動画 因数分解 ３次式の公式編の問題 19ch

三次方计算公式口诀 西瓜视频搜索

一般三次方程式的解 配立方 Youtube

26 P237r Training 96 7 Descubre Como Resolverlo En Qanda

3 Left 2 Left 3right Descubre Como Resolverlo En Qanda

完了しました 因数分解3 次 ニスヌーピー壁紙

3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す

式と証明 ３次式の因数分解について 日々是鍛錬 ひびこれたんれん

高校数学 ３次式の展開 因数分解 公式 覚え方 計算方法 学校よりわかりやすいサイト

3次方公式三次方分解因式重要公式 Kwame211的博客 Csdn博客 Azyvp

三次方程式とは 解き方 因数分解など や公式 グラフを解説 受験辞典

完了しました 因数分解3 次 ニスヌーピー壁紙

X的三次方怎么因式分解 百度经验

因式分解幽默教学 经典语录大全

３次以上の展開と因数分解はどうなる 公式の総まとめ

３次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ

分解因式方程的公式 三次方分解因式方法 三人行教育网 Www 3rxing Org

因数分解 発展 三次式の因数分解 Youtube

式と証明 ３次式の展開について 日々是鍛錬 ひびこれたんれん

高校数学 因数分解公式と3次式の因数分解 A B C 3abc 受験の月

列竖式进行因式分解 知乎

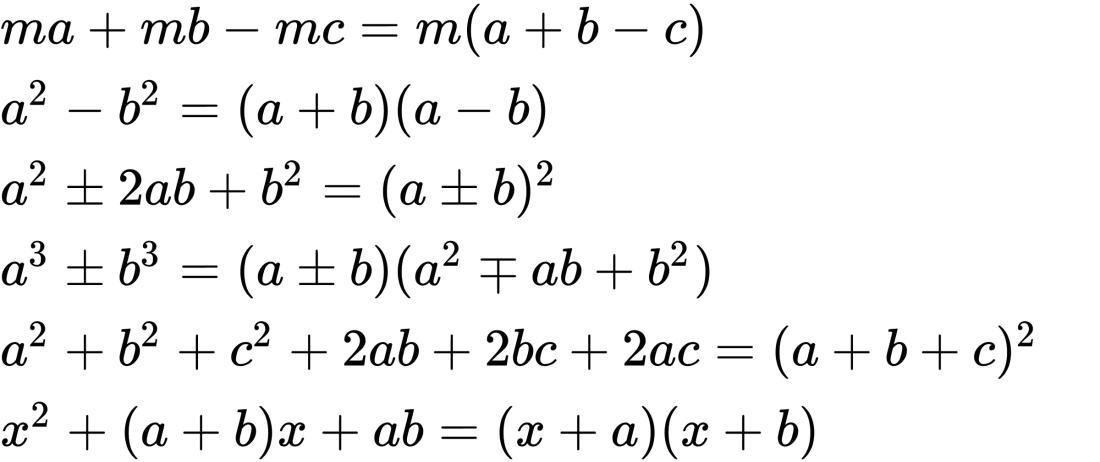
高校数学方程式3乗公式

乘法公式因式分解 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩xuite日誌

因式分解公式解因式分解 Oouzd

因数分解3 次 因数分解3次

複雑 な 因数 分解 展開の工夫と 2 難 順番の工夫 因数分解の利用 Amp Petmd Com

初三数学暑假班讲义第03讲 因式分解 教案 七七文库www 77wenku Com

3次式の因数分解 公式とやり方について問題を使って解説 数スタ

解方程 X 27x 54 0 立方和公式因式分解解题 哔哩哔哩 Bilibili

因式分解之待定係數法 一元三次多項式分解 每日頭條

2 3b觀念01因式分解三次多項式 為什麼我們需要牛頓定理 Youtube

文字が3つの因数分解 すうがくのいえ

立方差因式分解因式分解 立方和 Fpgab

三次式の因数分解の解法と押さえておきべき頻出公式

数と式の問題 京極一樹の数学塾

1

因式分解 整式的乘除与因式分解ppt课件2 Ppt课件下载 人人ppt

3分で分かる 因数分解の公式と解き方のコツ 練習問題と解説をわかりやすく 合格サプリ

三次项因式分解三次方分解因式方法

因式分解经典解析 人人焦点

因式分解技巧 二元二次的分解 星空暗流 博客园

高校数学 因数定理と３次式の因数分解 練習編 映像授業のtry It トライイット

三次多项式因式分解三次多项式因式分解有什么方法吗

Http Mail Knu Edu Tw Syokou Calculus Ch1 4 Pdf

高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium

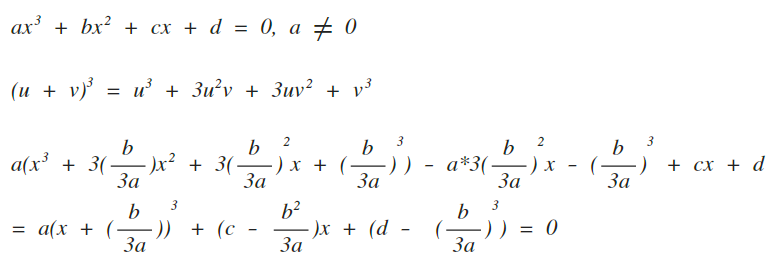
高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium

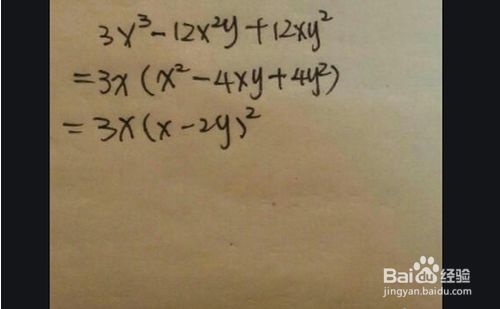
X的三次方怎么因式分解 百度经验

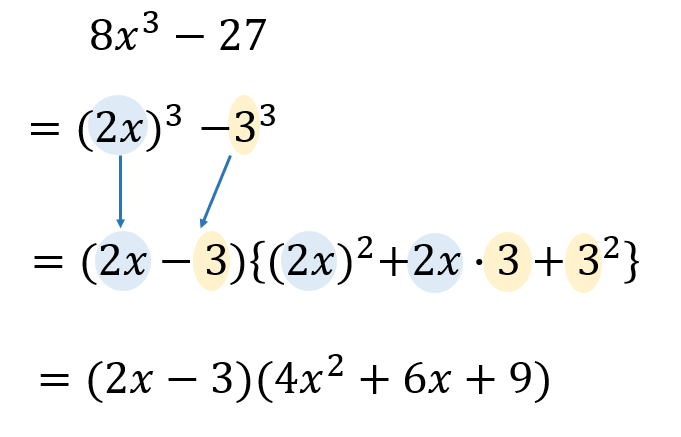
因式分解

初中数学 弄懂这几道题 从此使用完全平方公式因式分解得心应手

三次方 三次方程式展開

06一元二次方程的解法 三 公式法 因式分解法 知识讲解 提高 K12资源

因式分解

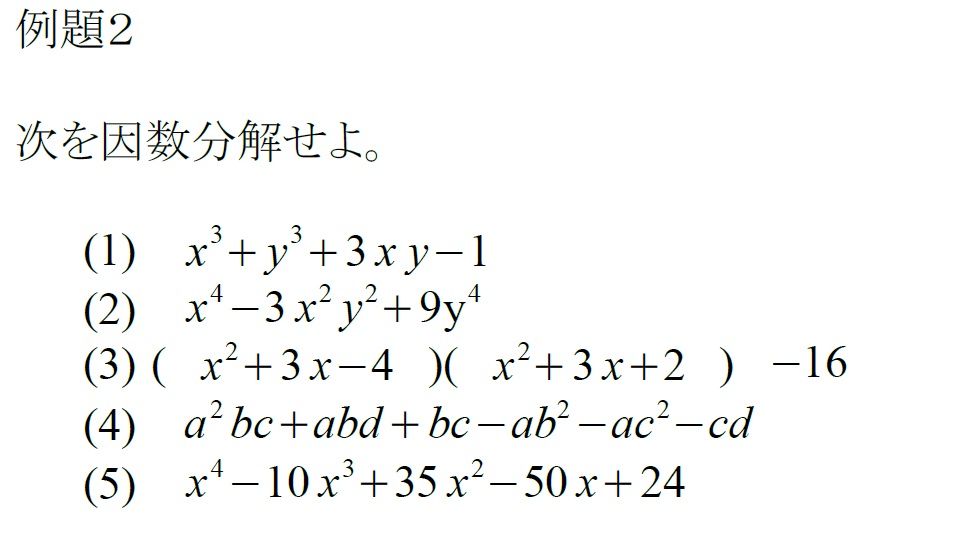
鉄則２ 数と式 因数分解 寺田の数学合格鉄則96に関するメモ

1 01的3次方分解 西瓜视频搜索

高校数学 因数分解公式と3次式の因数分解 受験の月

高次多项式的因式分解

因式分解

因式分解

3次式の因数分解 公式とやり方について問題を使って解説 数スタ

X 2 X 1因式分解 1减x的3次方怎么通分 X的三次方是奇函数吗

完了しました 因数分解3 次 ニスヌーピー壁紙

因式分解

最全初中因式分解公式 哔哩哔哩 つロ干杯 Bilibili

Incoming Term: 3次式 因数分解 公式,